Book to Programming With Zero Knowledge

Article Menu

/ajax/scifeed/subscribe

Open Access Article

ZPiE: Zero-Knowledge Proofs in Embedded Systems

Department of Information and Communication Technologies, Universitat Pompeu Fabra, 08002 Barcelona, Spain

^*

Author to whom correspondence should be addressed.

Academic Editors: Ioana Boureanu and Liqun Chen

Received: 9 September 2021 / Revised: 29 September 2021 / Accepted: 2 October 2021 / Published: 13 October 2021

Abstract

Zero-Knowledge Proofs (ZKPs) are cryptographic primitives allowing a party to prove to another party that the former knows some information while keeping it secret. Such a premise can lead to the development of numerous privacy-preserving protocols in different scenarios, like proving knowledge of some credentials to a server without leaking the identity of the user. Even when the applications of ZKPs were endless, they were not exploited in the wild for a couple of decades due to the fact that computing and verifying proofs was too computationally expensive. However, the advent of efficient schemes (in particular, zk-SNARKs) made this primitive to break into the scene in fields like cryptocurrencies, smart-contracts, and more recently, self-sovereign scenarios: private-by-design identity management and authentication. Nevertheless, its adoption in environments like the Internet of Things (IoT) remains unexplored due to the computational limitations of embedded systems. In this paper, we introduce ZPiE, a C library intended to create ZKP applications to be executed in embedded systems. Its main feature is portability: it can be compiled, executed, and used out-of-the-box in a wide variety of devices. Moreover, our proof-of-concept has been proved to work smoothly in different devices with limited resources, which can execute state-of-the-art ZKP authentication protocols.

1. Introduction

The inclusion of 5G communications [1] involves the deployment of network slices, dedicated physical and logical networks for different use cases such as the Internet of Things (IoT) [2]. In this scenario, 5G grants a large bandwidth and a low latency to be able to handle a large density of IoT devices. This fact has a big impact on the evolution of the smart-cities paradigm, where the amount of IoT devices is growing exponentially [3]. In that regard, exposure to cyberattacks like identity spoofing [4] is a big concern. To prevent this specific issue, several solutions have been designed, for instance, using physical unclonable functions [5], which has been proved to be a secure way to identify IoT devices. However, such authentication mechanisms cannot be completed with a single-message protocol, which introduces some latency to the scheme. Other solutions like in [6] present a way to authenticate IoT devices using Blockchains [7], distributed networks sharing a unique ledger containing transactions made by different nodes in the network. This builds a decentralized way to authenticate devices, which is also lightweight and applicable to a large number of scenarios.

However, even when most authentication mechanisms are secure against spoofing attacks, users' privacy is still an issue to be addressed. Examples of this are medical devices exchanging patients' private information, or autonomous cars sharing their location with a server. The common point between all these devices is that they need to share sensitive data over the network, data which should not be traced by any Internet Service Provider (ISP) or eavesdropper. Self-sovereign identity systems [8] become an essential feature to implement in this scenario: systems where users can control, access, and transparently consent their identities, preventing entities to track and collect their data. Research integrating such features into IoT environments has been conducted, like in [9], where the authors combine self-sovereign identity systems with distributed ledger technologies. The main elements required to get these features are Zero-Knowledge Proofs (ZKPs).

ZKPs are cryptographic primitives gaining a lot of momentum thanks to technologies such as Blockchain. While cryptocurrencies like Bitcoin [10] allow any node to review the transactions, knowing the sender, receiver, and the amount of exchanged money (among all the information involving the transaction), cryptocurrencies such as Zcash [11] use a specific ZKP scheme that allows its users to make anonymous payments. ZKPs allow a party (the prover) to prove to another party (the verifier) that he knows some information while keeping it secret. In other words, the sender, the receiver, and the amount of exchanged money is kept secret while everyone in the network agrees on the correctness of the transaction.

1.1. Motivation

Beyond cryptocurrencies, ZKPs are also used in protocols such as

SANS

[12], a privacy-preserving authentication scheme where users prove their right to access a service, based on some previously granted attributes. On the other hand, blockchains like Ethereum [13] provide an architecture capable of executing programs on-chain. These programs, called smart-contracts, can be combined with ZKP schemes to grant more privacy to its users: for instance, issuing a payment after using some service, while keeping the identity of the user secret. Protocols based on such approaches would be desirable in IoT scenarios, where many services are used, and most of them (such as medical applications) collect sensitive data. However, ZKP schemes require high computational resources, especially when the proof is generated. Even when current ZKP implementations do a great job in terms of efficiency, they are far from being portable, especially for embedded systems, as most of them focus on web applications, with the usage of programming languages like JavaScript, Webassembly, or Python. Some solutions [14] try to distribute the operations to be done to generate the proof between trusted servers. However, such approaches require a trusted environment and a persistent and fast connection with the server. Optimal solutions would be novel implementations focused on devices with low resources.

1.2. Contributions

We introduce

ZPiE

, a portable C library for generating and verifying ZKPs. As an initial proof-of-concept,

ZPiE

implements the specific ZKP construction called zk-SNARK. Our library provides a clear API to create proofs, and to verify them. Upon doing several tests on different devices, we have proved that, unlike other state-of-the-art solutions,

ZPiE

can be executed in

x86

,

x86_64

,

aarch64

and

arm32

CPU architectures out-of-the-box. In addition, after performing several experiments using a

x86_64

CPU (compatible with other state-of-the-art libraries) and comparing the results with other solutions, we have proved that

ZPiE

has similar performance. Furthermore, our solution can be easily integrated with existing implementations to be used in smart-contracts.

1.3. Roadmap

In Section 2 we survey the relevant use cases and libraries developed to work with ZKPs. In Section 3 we expose the building blocks required to understand the primitive we are implementing. In Section 4 we present

ZPiE

with all details. In Section 5 we include the performed experiments and their results. Conclusions and future work are provided in Section 6.

2. Related Work

In this section, we first introduce the main use cases of ZKPs. Later, we explain the different ZKP schemes and libraries used in real scenarios.

2.1. ZKP Use Cases

One of the main uses of ZKPs is enhancing privacy in cryptocurrencies. Along with the previously stated Zcash, other cryptocurrencies like Monero (https://www.getmonero.org/, accessed on 12 October 2021) use ZKPs to provide anonymous transactions when sending and receiving money over its network. Far from being limited to cryptocurrencies, ZKPs are used in Self-Sovereign Identity (SSI) systems as well, where users can control, consent, and widely use their identities among different services, along with other properties. A recent example of this is the solution introduced in [15], where authors introduce a Blockchain-based protocol combined with ZKPs, for enabling privacy-preserving authentication while removing the need for a central authority. They apply such an approach in electric vehicles scenarios, specifically when the vehicles need to charge the battery, and identification is requested by a charging provider.

Another recent research topic is introduced in

SANS

[12], where ZKPs could be used to authenticate users in scenarios like in 5G services. Such a protocol works as follows: upon signing up for using a 5G service, the service provider grants the user a digital signature signed by him, along with other parameters. Later, each time the user wants to use the service, he can do it anonymously: he computes a ZKP to demonstrate that he possesses a valid signature computed by the service provider, without leaking any other information. The service provider can validate the proof and grant the service without learning the identity of the user. Moreover, such an approach enhances privacy in distributed applications (DApps) as well. DApps are blockchain applications built using smart-contracts, which are binaries executed on-chain. For instance in Ethereum, such binaries are the result of compiling Solidity code (https://solidity.readthedocs.io/en/v0.5.3/, accessed on 12 October 2021). Like this, a program that verifies proofs could be executed on-chain. This technology can grant more privacy to users using different kinds of DApps, not solely using ZKPs but also using approaches like the one introduced in [16]. However, as stated, even when the verification is executed on-chain, the proof still needs to be computed by the proving device. As such, it is still hard to use DApps based on ZKPs on IoT devices due to its hardware limitations.

2.2. ZKP Schemes

Currently, there are several ZKP constructions used in the wild, each with its advantages and drawbacks. As shown in Table 1, one of the first efficient schemes was a zk-SNARK introduced in BSCTV'13 [17]. Such a scheme was later improved by the zk-SNARK introduced in Groth'16 [18], which is still one of the most efficient zk-SNARK schemes, especially when it comes to the verification algorithm. One of the main drawbacks of this kind of construction is the need for a trusted party that performs a trusted setup: a phase where some public parameters are generated, which will be used to generate and verify proofs. In this regard, Sonic [19] is a zk-SNARK that introduces a scheme where the setup can be updated for different circuits without the need to repeat the trusted setup generation. Another efficient zk-SNARK is Libra [20], which prover is guaranteed to outperform, even when the verifier does not have constant complexity. The most recent work on this topic was done by the authors in [21]. They introduce PlonK, a scheme with the same advantages that Sonic has, but improving the speed of the prover. Finally, recent research such as [22] shows a way to design a more efficient prover, while not compromising the verifier.

On the other hand, and beyond zk-SNARKs, we can find other ZKP schemes like Bulletproofs [23], which have the main advantage of not requiring a trusted setup. They are especially useful when the prover needs to compute a range proof [25], instead of an arithmetic circuit. Moreover, other concerns like post-quantum security have also arisen in the Zero-Knowledge field, and in this regard we have a scheme supposed to be post-quantum secure, called zk-STARKs (Zero-Knowledge Succinct Transparent ARgument of Knowledge) [24]. Post-quantum security is not a property of zk-SNARKs or Bulletproofs.

Finally, the soundness property of each of the schemes described relies on different security assumptions [26]. Most of the zk-SNARK constructions use a strong assumption called q-Power Knowledge of Exponent (q-PKE), which is not the best solution. On the other hand, Bulletproofs or zk-STARKs use better assumptions: the Discrete Logarithm Problem (DLP) and Collision Resistant Hash Functions (CRHF), respectively.

To develop ZKP applications, libraries like the one provided in this paper are required. One of the main libraries to accomplish this purpose is libsnark (https://github.com/scipr-lab/libsnark, accessed on 12 October 2021) a C++ library for constructing zk-SNARKs, which was used for some time by Zcash [11], based on the specific zk-SNARK construction introduced in [17], but supporting [18] as well, among others. Even when this library provides excellent benchmarks, one of the main drawbacks of this library, as the authors state, is not being well-optimized for ARM architectures.

Another library with similar benchmarks is bellman (https://github.com/zkcrypto/bellman/, accessed on 12 October 2021) implemented in Rust and meant for constructing zk-SNARKs, developed and currently used by Zcash.

Moreover, when it comes to developing DApps for the Ethereum blockchain, we previously stated that a verifier coded in Solidity is required. ZoKrates (https://github.com/Zokrates/ZoKrates, accessed on 12 October 2021) is a python toolbox for zk-SNARKs intended to generate Solidity verifiers, to be deployed into the Ethereum blockchain. Furthermore, a similar approach is snarkjs (https://github.com/iden3/snarkjs, accessed on 12 October 2021) a JavaScript library for constructing zk-SNARKs. It includes a clear API for generating trusted setups using a fairly secure MPC protocol, for generating proofs, and for verifying them. Plus, it also provides an easy way to export the verifier in Solidity, to deploy it into the Ethereum blockchain.

3. Building Blocks: zk-SNARKs

In this section, we introduce the required building blocks in regards to our solution. We do a high-level overview of how to construct a zk-SNARK (based on the construction introduced in [18]), which is also the scheme used in our proof-of-concept.

3.1. Preliminaries

A Zero-Knowledge Proof (ZKP) [27] is a cryptographic primitive which allows a prover P to convince a verifier V that a statement is true, without leaking any secret information. A statement is a set of elements known by both parties, defined as

$u\in \mathcal{L}$

, where

$\mathcal{L}$

is a Language. We have a witness w (the secret information only known by P) for a statement u if

$(u,w)\in \mathcal{R}$

, where

$\mathcal{R}$

is a polynomial-time decidable binary relation associated with

$\mathcal{L}$

. Formally speaking, ZKPs must satisfy 3 properties:

• Completeness: If the statement is true, P must be able to convince V.

• Soundness: If the statement is false, P must not be able to convince V that the statement is true, except with negligible probability.

• Zero-knowledge: V must not learn any information from the proof beyond the fact that the statement is true.

Moreover, V might request a proof of knowledge, a property to guarantee that P knows a witness w. Such a witness is a vector of elements for which a set of operations hold. These operations are defined by a graph composed of different wires and gates called circuit. Such a circuit leads to a set of equations representing the inputs and the outputs of these gates. The equations are also called constraints.

Even when first schemes required P and V to interact several times, Non-Interactive ZKPs (NIZKPs) [28] emerged, allowing P to prove statements to V by sending him a single message.

zk-SNARKs are Zero-Knowledge Succinct and Non-interactive ARguments of Knowledge [17]. They are the most used ZKPs, because they are short and succinct: the proofs can be verified in a few milliseconds. However, they require a trusted setup where some public parameters are generated. These parameters, called the Common Reference String (CRS), are used either by P and V to generate and verify proofs. In the process of generating the CRS, a secret randomness

$\tau$

is used, and such a randmoness should be destroyed afterwards. If an attacker gets

$\tau$

, the soundness property of the scheme breaks: the attacker would be able to compute false proofs that anyone could verify as if they were correct. As such, the CRS is commonly computed using a secure Multi-Party Computation (MPC) protocol [29], where

$\tau$

can only be leaked if all the participants are malicious. Therefore, zk-SNARKs are composed of three main algorithms: setup, prove and verify. The computing complexity of these algorithms depends on the number of operations that we do in the circuit, which is also the the number of gates n.

Regarding the security of zk-SNARKs, it mainly relies on the security of elliptic curves. Breaking the security of the elliptic curve used by a specific construction would lead to being able to generate false proofs and thus, breaking the soundness property of the scheme. Among the most used curves in ZKPs we have a Barreto-Naehrig curve [30] called BN128, which security level in practice is estimated to be 110-bits [31]. Another common curve in this scenario is BLS12-381 [11], which has around 128-bits of security, with the drawback of heavier group operations. More recent research is introduced in [32], where a new curve called BW6-761 is introduced. As stated by its authors, verification of proofs is at least five times faster than other state-of-the-art curves.

The zk-SNARK construction we will work on requires a pairing-friendly elliptic curve E over a finite field

${\mathbb{F}}_q$

, where q is a prime number, with the bilinear groups

$({\mathbb{G}}_1,{\mathbb{G}}_2,{\mathbb{G}}_T)$

of prime order r and a pairing

$e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$

being a bilinear map. We need the following generators: an element g being a generator for

${\mathbb{G}}_1$

, an element h being a generator for

${\mathbb{G}}_2$

, and

$e(g,h)$

being a generator for

${\mathbb{G}}_T$

. In order to represent group elements, we use the widely used additive notation: we write

${\left[a\right]}_1$

for

$g^a$

,

${\left[b\right]}_2$

for

$g^b$

, and

${\left[c\right]}_T$

for

$e{(g,h)}^c$

.

Arithmetic circuit. A circuit is a directed acyclic graph composed of different wires and gates, which lead to a set of equations relating the inputs and the outputs of these gates. The inputs and the output of this circuit, as well as the operations defined in the gates, are elements over a prime field

${\mathbb{F}}_r$

, where r is the order of E.

Rank 1 Constraint System. A Rank 1 Constraint System (R1CS) is a system of equations which checks the correctness of all the operations in our circuit, by grouping them in constraints. Each constraint is composed of a multiplicative gate with its two inputs and its output. Having a statement u and a witness w such that

$(u,w)\in \mathcal{R}$

, a R1CS is defined as a set of vectors

$(a,b,c)$

defining our circuit, whose solution is a vector

$s=(u,w)$

such that the following equation is satisfied:

$$\begin{array}{c}\hfill <a,s>·<b,s>-<c,s>=0\end{array}$$

(1)

Quadratic Arithmetic Program. A Quadratic Arithmetic Program (QAP) is a polynomial representation of the R1CS, which bundles all its constraints into one. It is a tuple of the polynomials

$(A,B,C,Z(x\left)\right)$

, where

$Z\left(x\right)$

divides

$A_i\left(x\right)·B_i\left(x\right)-C_i\left(x\right)$

without remainder. They satisfy the following equation:

$$\begin{array}{c}\hfill \sum _{i=0}^m{s}_i{A}_i\left(x\right))·\sum _{i=0}^m{s}_i{B}_i\left(x\right)-\sum _{i=0}^m{s}_i{C}_i\left(x\right)=H\left(x\right)Z\left(x\right)\end{array}$$

(2)

3.2. Protocol

Let

$\mathcal{R}$

be a relation composed of the elliptic curve E over

${\mathbb{F}}_q$

, the pairing e and a QAP

$(A,B,C,Z(x\left)\right)$

representing a circuit. The Groth'16 construction is divided into three algorithms (further details can be found in Appendix A), as depicted in Figure 1:

• $pk,vk\leftarrow Setup\left(\mathcal{R}\right)$

  : given the relation

  $\mathcal{R}$

  , the first step of the protocol generates a common reference string (CRS)

  $\sigma =({\left[{\sigma }_1\right]}_1,{\left[{\sigma }_2\right]}_2)$

  . From the CRS, some elements will be extracted into what we call the proving key

  $pk$

  , sent to the prover P to generate proofs. Moreover, other required elements will be taken into the verifying key

  $vk$

  , and sent to the verifier V to verify the proofs generated by P. In order to generate the CRS (i.e.,

  $pk$

  and

  $vk$

  ), a random set of values

  $\tau$

  is used. This

  $\tau$

  , also known as

  $trapdoor$

  , should be destroyed after performing the setup, as any party having

  $\tau$

  would be able to generate false proofs. To solve this last drawback, the setup must be generated by a trusted party (i.e., a set of entities performing a secure MPC protocol). In scenarios such as cryptocurrencies using zk-SNARKs (i.e., Zcash), an untrusty setup could lead to malicious parties using

  $\tau$

  to create false transactions, thus leading to losses of money.

• $\pi \leftarrow Prove(\mathcal{R},pk,u,w)$

  : the prover generates a proof

  $\pi =({\left[{\pi }_A\right]}_1,{\left[{\pi }_B\right]}_2,{\left[{\pi }_C\right]}_1)$

  , by multiplying u and w by some polynomials provided in

  $\sigma$

  . The prover also needs to compute the coefficients h of

  $H\left(x\right)$

  , which can be achieved in

  $O(nlogn)$

  using Fast Fourier Transform (FFT) techniques, as explained in detail in Appendix B. Then, h is multiplied by a polynomial provided in

  $\sigma$

  . The number of multi-exponentiations required to compute

  $\pi$

  are (note that multi-exponentiations in

  ${\mathbb{G}}_2$

  are more expensive than multi-exponentiations in

  ${\mathbb{G}}_1$

  ):

  –

  to compute

  ${\left[{\pi }_A\right]}_1$

  :

  $\left|u\right|+\left|w\right|$

  multi-exponentiations in

  ${\mathbb{G}}_1$

  .

  –

  to compute

  ${\left[{\pi }_B\right]}_2$

  :

  $\left|u\right|+\left|w\right|$

  multi-exponentiations in

  ${\mathbb{G}}_2$

  .

  –

  to compute

  ${\left[{\pi }_C\right]}_1$

  :

  $\left|u\right|+2·\left|w\right|+\left|h\right|$

  multi-exponentiations in

  ${\mathbb{G}}_1$

  .

• $0/1\leftarrow Verify(\mathcal{R},vk,u,\pi )$

  : the verifier accepts the proof (1) if an equation composed of three pairings [33] holds. Otherwise, the proof is rejected (0). Moreover, modifying a single bit of the proof leads to a proof that cannot be verified.

As such, the workflow of these algorithms in real applications would work as follows: we first need to compute the setup by means of a trusted party (step 1 in Figure 1). Later, this party shall share the required values with each of the involved parties, the prover and the verifier (step 2 in Figure 1). As shown in the steps 3 and 4, the prover computes the proof

$\pi$

and sends it to the verifier, who verifies it (step 5 in Figure 1). Steps 1 and 2 are performed only once, and later, the prover can compute as many proofs as he wants using the same values computed during the setup.

4. Our Solution: ZPiE

In this section, we provide all details regarding

ZPiE

. We start with a comprehensive explanation about how it was designed, to later move to the technical details. We later provide the techniques used to improve the efficiency of the code. Finally, we provide an explanation on how to use the library.

4.1. Design

Our solution (https://github.com/xevisalle/zpie, accessed on 12 October 2021) has been designed to provide a clear interface for developing ZKP applications. As such, it provides an API to design circuits, perform the setup phase, generate proofs, and verify them. Furthermore, our solution can easily integrate the verifier in Solidity applications (i.e., using ZoKrates or snarkjs), in order to deploy smart-contracts into the Ethereum network.

ZPiE

can be used in devices with very low resources like a Raspberry Pi Zero, and in a wide variety of CPU architectures:

x86

,

x86_64

,

aarch64

, and

arm32

.

4.2. Implementation

Our solution has been designed with portability and scalability in mind. For such a reason, we decided to use C to code it, which is still widely used in embedded systems, and allows us full control over the hardware resources. For dealing with big numbers we use GNU GMP (https://gmplib.org/, accessed on 12 October 2021) which is one of the fastest approaches to do operations with large numbers in C. For the group operations over elliptic curves, and pairings, we rely on the MCL library (https://github.com/herumi/mcl, accessed on 12 October 2021), a well-optimized set of functions that offer us support for all the operations we need to perform. Both GMP and MCL offer support for

x86

,

x86_64

,

aarch64

, and

arm32

CPU architectures. Moreover, all the code has been designed to split the workload into threads, to increase the performance especially when the prover is executed in a multicore CPU. Regarding the circuit design, either the circuit parser and the circuit' code developed by the user are coded in pure C, so they are both compiled altogether along with all the other code for maximum performance.

4.3. Efficiency

The first step to being able to use our proof system is to generate the CRS through the setup algorithm. Using Groth'16, the setup has a complexity of

$O\left(n\right)$

, so we need to compute a number of elements that depends only on the size of the circuit. Regarding the verifier, where the complexity time is constant (

$O\left(1\right)$

), he only needs to compute 3 pairings and verify that an equation holds, which is not expensive in terms of power consumption. Plus, the operations which require more power consumption are done by the prover when computing the proof. That is computing the h coefficients, and doing the multi-exponentiations in

${\mathbb{G}}_1$

and

${\mathbb{G}}_2$

.

4.3.1. Computing h Coefficients

As stated in Appendix B, we rely on a FFT function to compute the coefficients in

$O(nlogn)$

. Our FFT function has been designed to be as efficient as possible. The size of the domain used for the FFTs in

$N_e=2^l$

, where l is a big integer, so

$\left|h\right|=N_e$

. In total, the prover has to perform 3 inverse FFTs over a domain S, 3 FFTs over a shifted domain T, and one last inverse FFT over T. As depicted in Figure 2, this set of operations is, for any number of constraints, the same small percentage of all the operations performed to generate the proof.

4.3.2. Multi-Exponentiations

Our solution uses three different multi-exponentiation approaches: the naive multi-exponentiation (which is a serial approach), the multi-exponentiation function provided MCL, and a Bos-Coster multi-exponentiation algorithm (further details provided in Appendix C). While the former achieves the worst results, MCL gets better marks. However, our Bos-Coster implementation achieves the best results. We split the Bos-Coster operations into chunks to increase the performance when using multithreading. As depicted in Figure 2, the multi-exponentiations represent a huge percentage of the operations to be done. In addition, the heap sorting, a step required after each Bos-Coster execution, increases exponentially in terms of global percentage.

4.4. Applications

Some of the use cases of ZKPs involve proving to another party that we know the preimage of a hashed value, or that we have a valid signature for a secret message. We implemented both approaches using

ZPiE

, and provide an API to easily use them.

To use our library, we need to write a circuit which will be parsed later. To do so, Listing 1 shows an example on how to compute the MiMC [34] hash of a preimage

$x_{i}n$

. As can be seen, we set a public output h, the hash of the secret preimage

$x_{i}n$

(in such a process some randomness k is used as well). In other words, this circuit will compute a proof that, once verified, the verifier will be sure that who computed the proof knows

$x_{i}n$

. As can be seen in Listing 2,

ZPiE

can compute the setup, the proof, and verify it by simply executing each algorithm as shown in the snippet.

In addition, and as shown in Listing 3,

ZPiE

can easily verify an EdDSA [35] signature by calling the function

verify_eddsa(\dots)

, providing the required parameters as shown in the snippet. In this scenario, the prover is proving to the verifier that he knows a valid signature for some secret message. In such regard, the code can be modified depending on the use case, to select which values are public or secret.

Listing1.

Circuit example for computing the MiMC hash of a preimage.

Listing2.

Program execution example.

Listing3.

Circuit example for computing 16,384 constraints.

5. Experiments and Results

In this section, we perform several experiments to prove the efficiency of our solution. In order to do so, we implemented a circuit composed of 16,384 constraints as shown in Listing 4.

Listing4.

Circuit example for computing 16,384 constraints.

As stated previously, zk-SNARKs are composed of three algorithms. The setup is performed only once, so the performance of this algorithm is not of big importance in practice. However, using

ZPiE

, the setup of a circuit of 16,384 constraints can be performed in 17 s using a laptop CPU in single-thread. Regarding the proof verification, our zk-SNARK construction has a succinct verifier which verifies any proof in just 0.0011 s.

Moreover, we performed several experiments to prove the performance of

ZPiE

when computing proofs. First, we compared our solution with a well-optimized library intended to generate proofs in desktop applications, libsnark. As depicted in Figure 3,

ZPiE

achieves great results, similar to the ones achieved by libsnark, either in single or multi-thread modes.

Then, as depicted in Figure 4, we executed our solution with different constraint amounts in two different processors, either in single and multi-thread modes. As can be seen, the laptop processor i7-11370H (

x86_64

) achieves excellent results either in single or multi-thread modes. Regarding the mobile processor Snapdragon 845 (

aarch64

), the results are still excellent in multi-thread. In single-thread mode, the difference is bigger, yet the proofs can still be executed in a fairly small amount of time.

Furthermore, we successfully computed proofs using a Raspberry Pi Zero W, which CPU architecture is ARM6l (

arm32

) and has a very low clock frequency (700 MHz). As depicted in Figure 5, the results are much higher than using mobile or desktop processors, yet the proofs can still be executed. As such, ZKP applications could be executed in embedded devices, at least when speed is not of paramount importance. For instance, protocols such as

SANS

, which needs around 5000 constraints, could be executed in less than a minute using a Raspberry Pi Zero W. This allows IoT devices to use privacy-preserving protocols based on zk-SNARKs.

6. Conclusions

In this paper, we introduced a novel library intended to generate Zero-Knowledge Proofs in devices with low computing resources. After performing several experiments, the results prove how zk-SNARKs can be computed using processors such as the ARM11 of a Raspberry Pi Zero W. After stating the need for privacy-preserving protocols that use zk-SNARKs in IoT scenarios, we demonstrated that their development and execution in such devices is feasible.

ZPiE

allows us to develop ZKP applications in embedded devices, by using the specific Groth'16 zk-SNARK. However, we have seen how other schemes exist, each having different features. Implementing other schemes for embedded devices would be an interesting future work to do, in order to expand the uses cases of ZKPs in IoT devices. Overall, being able to use ZKPs in IoT devices should open the door to designing and implementing more protocols for IoT devices based on ZKPs, not solely for authentication purposes but also for any other privacy matter where ZKPs could be useful.

Moreover, even when we get excellent results, there is still room for improvement. It would be interesting to work on boosting even further the performance of

ZPiE

, by testing other elliptic curve libraries rather than MCL, or by designing new algorithms to reduce the overhead of the executions. Moreover, allowing users to speed up the library using GPUs would be another interesting feature to implement, to allow the usage of our library in scenarios other than IoT devices.

Author Contributions

Conceptualization, X.S.; methodology, X.S.; software, X.S.; investigation, X.S.; writing—original draft preparation, X.S.; writing—review and editing, X.S. and V.D.; supervision, V.D.; project administration, V.D.; funding acquisition, V.D. Both authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Project RTI2018-102112-B-100 (AEI/FEDER, UE) and H2020 PRESENT Grant Agreement Nº 856879.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

ZKP	Zero-Knowledge Proof
IoT	Internet of Things
ISP	Internet Service Provider
DApps	Distributed Applications
DLP	Discrete Logarithm Problem
CRHF	Collision-Resistant Hash Functions
NIZKP	Non-Interactive Zero-Knowledge Proofs
CRS	Common Reference String
MPC	Multi-Party Computation
R1CS	Rank 1 Constraint System
QAP	Quadratic Arithmetic Program
FFT	Fast Fourier Transform

List of Mathematical Symbols

The following mathematical symbols are used in this manuscript:

u	Statement
$\mathcal{L}$	Language
w	Witness
$\mathcal{R}$	Relation
$\tau$	Secret randomness
E	Elliptic curve
$\mathbb{F}$	Finite field
q	Prime number
$\mathbb{G}$	Group
e	Pairing
g	Generator of ${\mathbb{G}}_1$
h	Generator of ${\mathbb{G}}_2$
r	Order of the elliptic curve group
$\sigma$	Elements of the Common Reference String
$\pi$	Proof
l	Big integer
$N_e$	Size of the domain used for the FFTs
T	Shifted domain

Appendix A. Groth'16

Let

$\mathcal{R}$

be a relation composed of the elliptic curve E over

${\mathbb{F}}_q$

, the pairing e and a QAP

$(A,B,C,Z(x\left)\right)$

representing a circuit. The Groth'16 construction is divided into three algorithms:

• $\sigma \leftarrow Setup\left(\mathcal{R}\right)$

  : To perform the setup, we pick

  $\alpha ,\beta ,\gamma ,\delta ,x$

  from

  ${\mathbb{F}}_r$

  and define

  $\tau =(\alpha ,\beta ,\gamma ,\delta ,x)$

  . Later we compute

  $\sigma =({\left[{\sigma }_1\right]}_1,{\left[{\sigma }_2\right]}_2)$

  :

  $$\begin{array}{c}\hfill v{k}^{\prime }={\{\frac{\beta A_i\left(x\right)+\alpha B_i\left(x\right)+C_i\left(x\right)}{\gamma }\}}_{i=0}^l\\ \hfill p{k}^{\prime }={\{\frac{\beta A_i\left(x\right)+\alpha B_i\left(x\right)+C_i\left(x\right)}{\delta }\}}_{i=l+1}^m\\ \hfill {\sigma }_1=(\alpha ,\beta ,\delta ,{\{x^i\}}_{i=0}^{n-1},v{k}^{\prime },p{k}^{\prime },{\{\frac{x^{i}t\left(x\right)}{\delta }\}}_{i=0}^{n-2})\end{array}$$

  (A1)

  $${\sigma }_2=(\beta ,\gamma ,\delta ,{\left\{x^i\right\}}_{i=0}^{n-1})$$

  (A2)

• $\pi \leftarrow Prove(\mathcal{R},\sigma ,s)$

  The prover randomly picks

  $r,c$

  in

  ${\mathbb{F}}_r$

  and computes

  $\pi =({\left[{\pi }_A\right]}_1,$ ${\left[{\pi }_B\right]}_2,{\left[{\pi }_C\right]}_1)$

  :

  $$\begin{array}{c}\hfill {\pi }_A=\alpha +\sum _{i=0}^m{s}_i{A}_i\left(x\right)+r\delta \\ \hfill {\pi }_B=\beta +\sum _{i=0}^m{s}_i{B}_i\left(x\right)+c\delta \\ \hfill {\pi }_C^{\prime }=\frac{{\sum }_{i=l+1}^m{s}_i(\beta A_i\left(x\right)+\alpha B_i\left(x\right)+C_i\left(x\right))+h\left(x\right)t\left(x\right)}{\delta }\\ \hfill {\pi }_C={\pi }_C^{\prime }+{\pi }_{A}c+{\pi }_{B}r-rc\delta \end{array}$$

  (A3)

• $0/1\leftarrow Verify(\mathcal{R},\sigma ,u,\pi )$

  : the verifier accepts the proof iff the following equation holds:

  $$\begin{array}{c}\hfill {\left[p_1\right]}_T={\left[{\pi }_A\right]}_1·{\left[{\pi }_B\right]}_2\\ \hfill [p_2{]}_T={\left[\alpha \right]}_1·{\left[\beta \right]}_2\\ \hfill [p_3{]}_T=\sum _{i=0}^l{s}_i{[\frac{\beta A_i\left(x\right)+\alpha B_i\left(x\right)+C_i\left(x\right)}{\gamma }]}_1·{\left[\gamma \right]}_2\\ \hfill [p_4{]}_T={\left[C\right]}_1·{\left[\delta \right]}_2\\ \hfill [p_1{]}_T={\left[p_2\right]}_T+{\left[p_3\right]}_T+{\left[p_4\right]}_T\end{array}$$

  (A4)

Appendix B. FFT Techniques for Computing h Coefficients

Our QAP is a 3-matrix set of size

$N\times M$

. Working on

${\mathbb{F}}_r$

, where r is a prime number and the order of the used elliptic curve, we find a generator g for our field. Having this, we find two values k and an extended size for N, called

$N_e=2^l$

(where l is an integer `large enough') such that

$r=k{N}_e+1$

. As can be seen,

$N_e$

is a power of 2, as 2-addicity is a desirable property for more efficient FFT algorithms. With this, now we can find our

$N_e$

th primitive root of unity:

This generates our domain:

$$S=\{1,\omega ,\dots ,{\omega }^{N_e-1}\}$$

(A6)

Now we need to compute three polynomials

$A\left(z\right)=\{A_0,\dots ,A_{M-1}\},B\left(z\right)=\{B_0,\dots ,B_{M-1}\},C\left(z\right)=\{C_0,\dots ,C_{M-1}\}$

, where z is our toxic waste x defined in the Groth setup:

$$\begin{array}{c}\hfill A_i\left(z\right)=\sum _{j=0}^{N_e-1}{L}_{i,j}·{\displaystyle \frac{La{g}_j\left(z\right)}{z-S_j}}\\ \hfill B_i\left(z\right)=\sum _{j=0}^{N_e-1}{R}_{i,j}·{\displaystyle \frac{La{g}_j\left(z\right)}{z-S\left(j\right)}}\\ \hfill C_i\left(z\right)=\sum _{j=0}^{N_e-1}{O}_{i,j}·{\displaystyle \frac{La{g}_j\left(z\right)}{z-S\left(j\right)}}\end{array}$$

(A7)

where

$$\begin{array}{c}\hfill La{g}_1\left(z\right)={\displaystyle \frac{z^{N_e}-1}{N_e}}\\ \hfill La{g}_{j+1}\left(z\right)=\omega La{g}_j\left(z\right)\end{array}$$

(A8)

As such, the setup has defined three polynomials

$A\left(x\right),B\left(x\right),C\left(x\right)$

. Now, using a solution to our circuit w the prover computes the following values:

$$\begin{array}{c}\hfill A=\sum _{i=0}^{M-1}{A}_i·w_i\\ \hfill B=\sum _{i=0}^{M-1}{B}_i·w_i\\ \hfill C=\sum _{i=0}^{M-1}{C}_i·w_i\end{array}$$

(A9)

Now, the prover computes the evaluation of three polynomials:

$$\begin{array}{c}\hfill A_j=\sum _{i=0}^{M-1}{L}_{i,j}·w_i\\ \hfill B_j=\sum _{i=0}^{M-1}{R}_{i,j}·w_i\\ \hfill C_j=\sum _{i=0}^{M-1}{O}_{i,j}·w_i\end{array}$$

(A11)

Now, the prover will use

$A\left(z\right),B\left(z\right),C\left(z\right)$

to compute the coefficients h of

$H\left(x\right)$

:

$$H\left(x\right)={\displaystyle \frac{A\left(x\right)B\left(x\right)-C\left(x\right)}{Z\left(x\right)}}$$

(A12)

In order to do so, the prover selects a random

$\sigma$

and computes a shifted domain

$T=\{\sigma ,\sigma \omega ,\dots ,\sigma {\omega }^{N_e-1}\}$

. He also sets

$Z={\sigma }^{N_e}-1$

and does what follows:

• Computes 3 IFFTs in our domain S:

  $$\begin{array}{c}\hfill A_S=IFFT(A,S)\\ \hfill B_S=IFFT(B,S)\\ \hfill C_S=IFFT(C,S)\end{array}$$

  (A13)

• Computes 3 FFTs in our domain T:

  $$\begin{array}{c}\hfill A_T=FFT(A_S,T)\\ \hfill B_T=FFT(B_S,T)\\ \hfill C_T=FFT(C_S,T)\end{array}$$

  (A14)

• Computes

  $H={\displaystyle \frac{A_T{B}_T-C_T}{Z}}$

  point by point.

• Computes the shifted coefficients

  $h_T=IFFT(H,T)$

  and it finally gets

  $h=h_T/\sigma$

  point by point.

Appendix C. Bos-Coster

Let the pairs

$(s_1,P_1),(s_2,P_2),\dots ,(s_n,P_n)$

be the elements of the multi-exponentiations to perform. We sort the list from large to small

$s_i$

, by means of a well-optimised binary heap. Then, while the list is larger than 1:

• $(s_1,P_1)=(s_1-s_2,P_1)$

• $(s_2,P_2)=(s_2,P_1+P_2)$

• if

  $s_1=0$

  , we remove this pair

• We sort the list again

When only one pair remains,

$s_1{P}_1$

is our solution.

References

1. Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; De Silva, P.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
2. He, K.; Wang, Z.; Li, D.; Zhu, F.; Fan, L. Ultra-reliable MU-MIMO detector based on deep learning for 5G/B5G-enabled IoT. Phys. Commun. 2020, 43, 101181. [Google Scholar] [CrossRef]
3. Painuly, S.; Kohli, P.; Matta, P.; Sharma, S. Advance applications and future challenges of 5G IoT. In Proceedings of the 2020 3rd International Conference on Intelligent Sustainable Systems (ICISS), Palladam, India, 3–5 December 2020; pp. 1381–1384. [Google Scholar] [CrossRef]
4. Mohammadnia, H.; Slimane, S.B. IoT-NETZ: Practical spoofing attack mitigation approach in SDWN network. In Proceedings of the 2020 Seventh International Conference on Software Defined Systems (SDS), Paris, France, 30 June–3 July 2020; pp. 5–13. [Google Scholar] [CrossRef]
5. Kim, B.; Yoon, S.; Kang, Y.; Choi, D. PUF based IoT device authentication scheme. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 16–18 October 2019; pp. 1460–1462. [Google Scholar] [CrossRef]
6. Khalid, U.; Asim, M.; Baker, T.; Hung, P.C.; Tariq, M.A.; Rafferty, L. A decentralized lightweight blockchain-based authentication mechanism for IoT systems. Clust. Comput. 2020, 1–21. [Google Scholar] [CrossRef]
7. Leible, S.; Schlager, S.; Schubotz, M.; Gipp, B. A Review on Blockchain Technology and Blockchain Projects Fostering Open Science. Front. Blockchain 2019, 2, 16. [Google Scholar] [CrossRef]
8. Sovrin Foundation. Sovrin: A Protocol and Token for Self-Sovereign Identity and Decentralized Trust. 2018. Available online: https://sovrin.org/wp-content/uploads/Sovrin-Protocol-and-Token-White-Paper.pdf (accessed on 28 September 2021).
9. Luecking, M.; Fries, C.; Lamberti, R.; Stork, W. Decentralized identity and trust management framework for internet of things. In Proceedings of the 2020 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Toronto, ON, Canada, 2–6 May 2020; pp. 1–9. [Google Scholar] [CrossRef]
10. Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2009. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3440802 (accessed on 20 August 2021).
11. Hopwood, D.; Bowe, S.; Hornby, T.; Wilcox, N. Zcash Protocol Specification— Version 2019.0.2. 2019. Available online: https://github.com/zcash/zips/blob/master/protocol/protocol.pdf (accessed on 28 September 2021).
12. Salleras, X.; Daza, V. SANS: Self-Sovereign Authentication for Network Slices. Secur. Commun. Netw. 2020, 2020. [Google Scholar] [CrossRef]
13. Wood, D. Ethereum: A Secure Decentralised Generalised Transaction Ledger. 2014. Available online: https://files.gitter.im/ethereum/yellowpaper/VIyt/Paper.pdf (accessed on 16 April 2021).
14. Wu, H.; Zheng, W.; Chiesa, A.; Popa, R.A.; Stoica, I. DIZK: A distributed zero knowledge proof system. In Proceedings of the 27th USENIX Security Symposium (USENIX Security 18), Baltimore, MD, USA, 15–17 August 2018; pp. 675–692. [Google Scholar]
15. Gabay, D.; Akkaya, K.; Cebe, M. Privacy-Preserving Authentication Scheme for Connected Electric Vehicles Using Blockchain and Zero Knowledge Proofs. IEEE Trans. Veh. Technol. 2020, 69, 5760–5772. [Google Scholar] [CrossRef]
16. Sestrem Ochôa, I.; Reis Quietinho Leithardt, V.; Calbusch, L.; De Paz Santana, J.F.; Delcio Parreira, W.; Oriel Seman, L.; Albenes Zeferino, C. Performance and Security Evaluation on a Blockchain Architecture for License Plate Recognition Systems. Appl. Sci. 2021, 11, 1255. [Google Scholar] [CrossRef]
17. Ben-Sasson, E.; Chiesa, A.; Tromer, E.; Virza, M. Succinct non-interactive zero knowledge for a von neumann architecture. In Proceedings of the 23rd USENIX Security Symposium (USENIX Security 14), San Diego, CA, USA, 20–22 August 2014; pp. 781–796. [Google Scholar]
18. Groth, J. On the size of pairing-based non-interactive arguments. In Advances in Cryptology—EUROCRYPT 2016; Fischlin, M., Coron, J.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 305–326. [Google Scholar]
19. Maller, M.; Bowe, S.; Kohlweiss, M.; Meiklejohn, S. Sonic: Zero-knowledge SNARKs from linear-size universal and updatable structured reference strings. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2111–2128. [Google Scholar] [CrossRef]
20. Xie, T.; Zhang, J.; Zhang, Y.; Papamanthou, C.; Song, D. Libra: Succinct zero-knowledge proofs with optimal prover computation. In Advances in Cryptology—CRYPTO 2019; Boldyreva, A., Micciancio, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 733–764. [Google Scholar]
21. Gabizon, A.; Williamson, Z.J.; Ciobotaru, O. PLONK: Permutations over Lagrange-Bases for Oecumenical Noninteractive Arguments of Knowledge. Cryptology ePrint Archive, Report 2019/953. 2019. Available online: https://ia.cr/2019/953 (accessed on 28 September 2021).
22. Lee, J.; Setty, S.; Thaler, J.; Wahby, R. Linear-Time and Post-Quantum Zero-Knowledge SNARKs for R1CS. Cryptology ePrint Archive, Report 2021/030. 2021. Available online: https://ia.cr/2021/030 (accessed on 28 September 2021).
23. Bünz, B.; Bootle, J.; Boneh, D.; Poelstra, A.; Wuille, P.; Maxwell, G. Bulletproofs: Short proofs for confidential transactions and more. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; pp. 315–334. [Google Scholar] [CrossRef]
24. Ben-Sasson, E.; Bentov, I.; Horesh, Y.; Riabzev, M. Scalable, Transparent, and Post-Quantum Secure Computational Integrity. Cryptology ePrint Archive, Report 2018/046. 2018. Available online: https://eprint.iacr.org/2018/046 (accessed on 28 September 2021).
25. Morais, E.; Koens, T.; Van Wijk, C.; Koren, A. A survey on zero knowledge range proofs and applications. SN Appl. Sci. 2019, 1, 1–17. [Google Scholar] [CrossRef]
26. Goldwasser, S.; Tauman Kalai, Y. Cryptographic assumptions: A position paper. In Theory of Cryptography; Kushilevitz, E., Malkin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 505–522. [Google Scholar]
27. Goldwasser, S.; Micali, S.; Rackoff, C. The knowledge complexity of interactive proof-systems. In Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing, Providence, RI, USA, 6–8 May 1985; ACM: New York, NY, USA, 1985; pp. 291–304. [Google Scholar] [CrossRef]
28. Blum, M.; Feldman, P.; Micali, S. Non-interactive zero-knowledge and its applications. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; ACM: New York, NY, USA, 1988; pp. 103–112. [Google Scholar] [CrossRef]
29. Bowe, S.; Gabizon, A.; Miers, I. Scalable Multi-Party Computation for zk-SNARK Parameters in the Random Beacon Model. Cryptology ePrint Archive, Report 2017/1050. 2017. Available online: https://eprint.iacr.org/2017/1050 (accessed on 28 September 2021).
30. Barreto, P.S.L.M.; Naehrig, M. Pairing-friendly elliptic curves of prime order. In Selected Areas in Cryptography; Preneel, B., Tavares, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 319–331. [Google Scholar]
31. Menezes, A.; Sarkar, P.; Singh, S. Challenges with Assessing the Impact of NFS Advances on the Security of Pairing-Based Cryptography. Cryptology ePrint Archive, Report 2016/1102. 2016. Available online: https://eprint.iacr.org/2016/1102 (accessed on 28 September 2021).
32. El Housni, Y.; Guillevic, A. Optimized and secure pairing-friendly elliptic curves suitable for one layer proof composition. In Cryptology and Network Security; Krenn, S., Shulman, H., Vaudenay, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 259–279. [Google Scholar]
33. Beuchat, J.L.; González-Díaz, J.E.; Mitsunari, S.; Okamoto, E.; Rodríguez-Henríquez, F.; Teruya, T. High-speed software implementation of the optimal ate pairing over Barreto–Naehrig curves. In Pairing-Based Cryptography—Pairing 2010; Joye, M., Miyaji, A., Otsuka, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 21–39. [Google Scholar]
34. Albrecht, M.; Grassi, L.; Rechberger, C.; Roy, A.; Tiessen, T. MiMC: Efficient encryption and cryptographic hashing with minimal multiplicative complexity. In Advances in Cryptology—ASIACRYPT 2016; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 191–219. [Google Scholar]
35. Bernstein, D.J.; Duif, N.; Lange, T.; Schwabe, P.; Yang, B.Y. High-Speed High-Security Signatures. J. Cryptogr. Eng. 2012, 2. Available online: https://cr.yp.to/papers.html#ed25519 (accessed on 28 September 2021). [CrossRef]

Figure 1. Zero-Knowledge Proof System.

Figure 1. Zero-Knowledge Proof System.

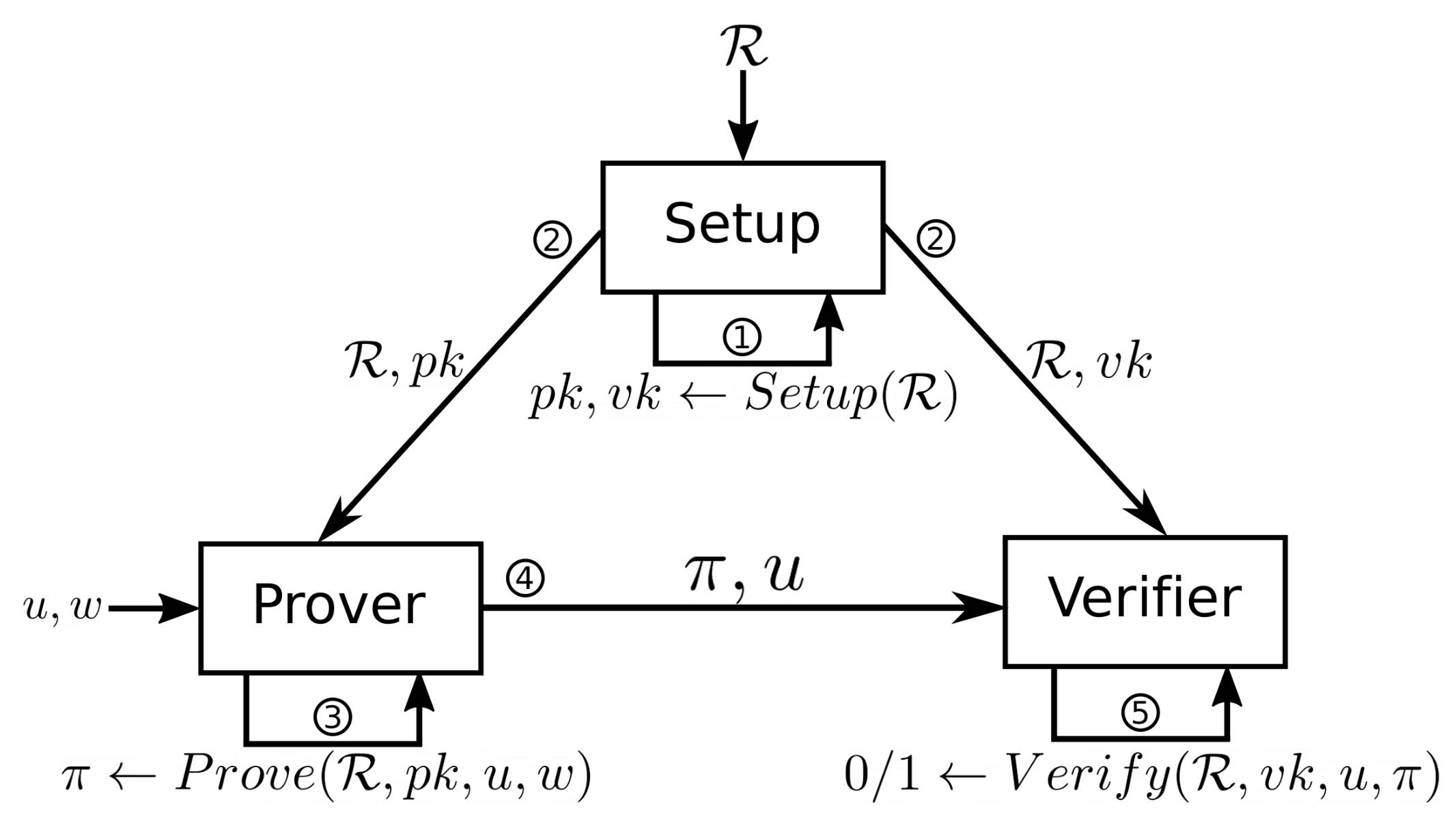
Figure 2. CPUs proving operations workload comparison of ZPiE executed in a i7-11370H CPU in single-thread mode. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

Figure 2. CPUs proving operations workload comparison of ZPiE executed in a i7-11370H CPU in single-thread mode. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

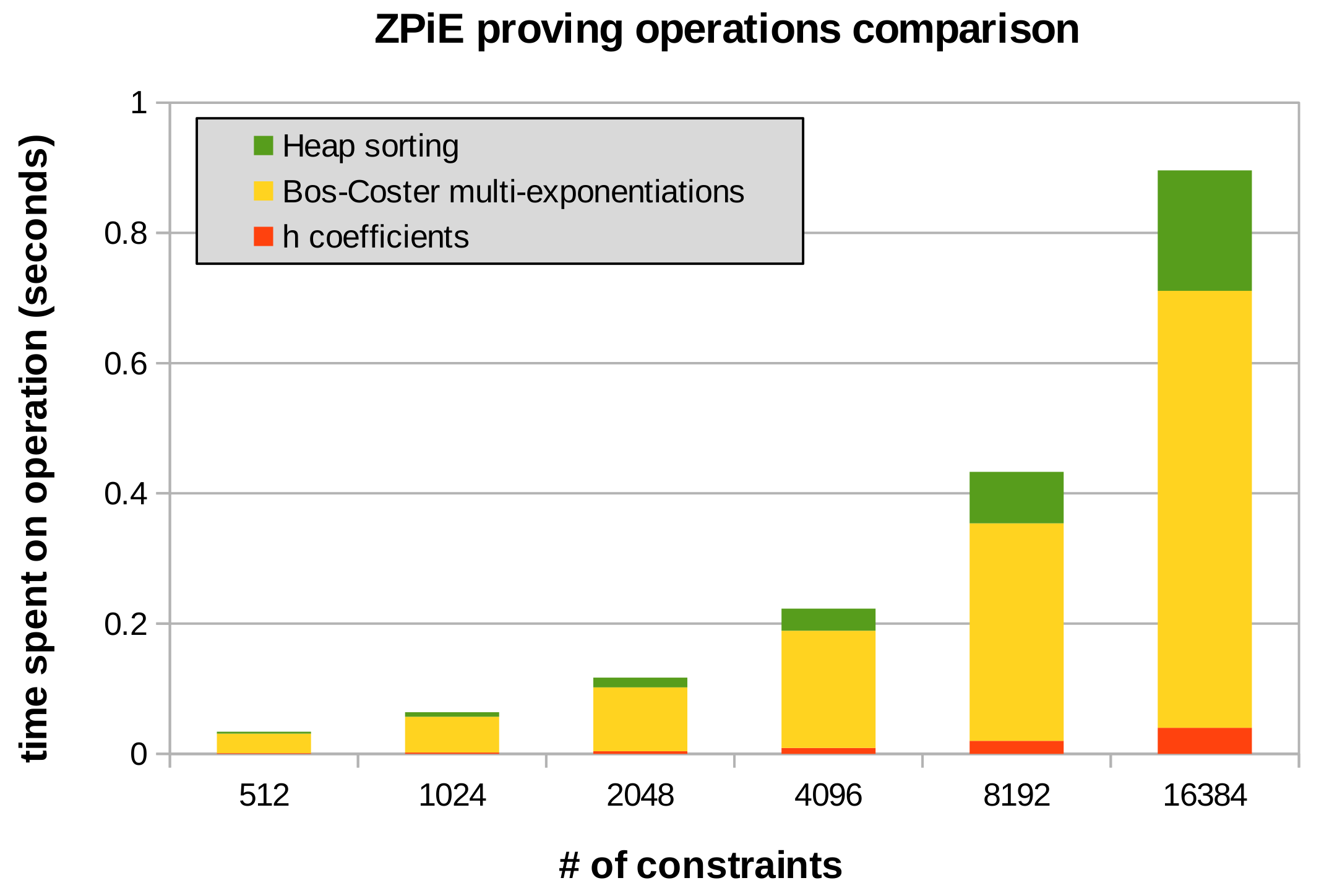
Figure 3. ZPiE and libsnark proving times comparison using different constraint amounts, single-thread and multi-thread modes. All the tests are executed using a i7-11370H CPU. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

Figure 3. ZPiE and libsnark proving times comparison using different constraint amounts, single-thread and multi-thread modes. All the tests are executed using a i7-11370H CPU. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

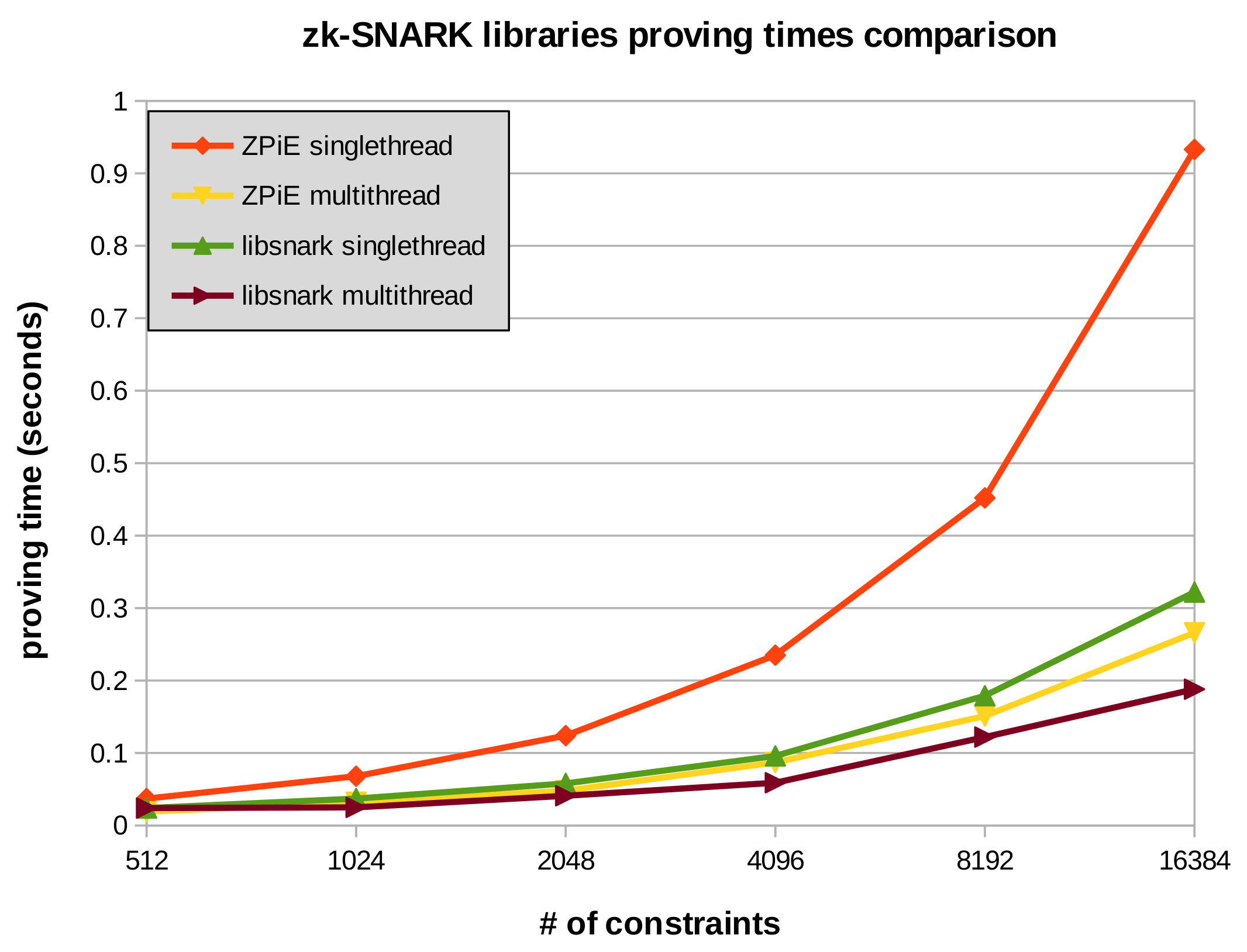
Figure 4. CPUs proving times comparison of ZPiE using different constraint amounts, single-thread and multi-thread modes. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

Figure 4. CPUs proving times comparison of ZPiE using different constraint amounts, single-thread and multi-thread modes. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

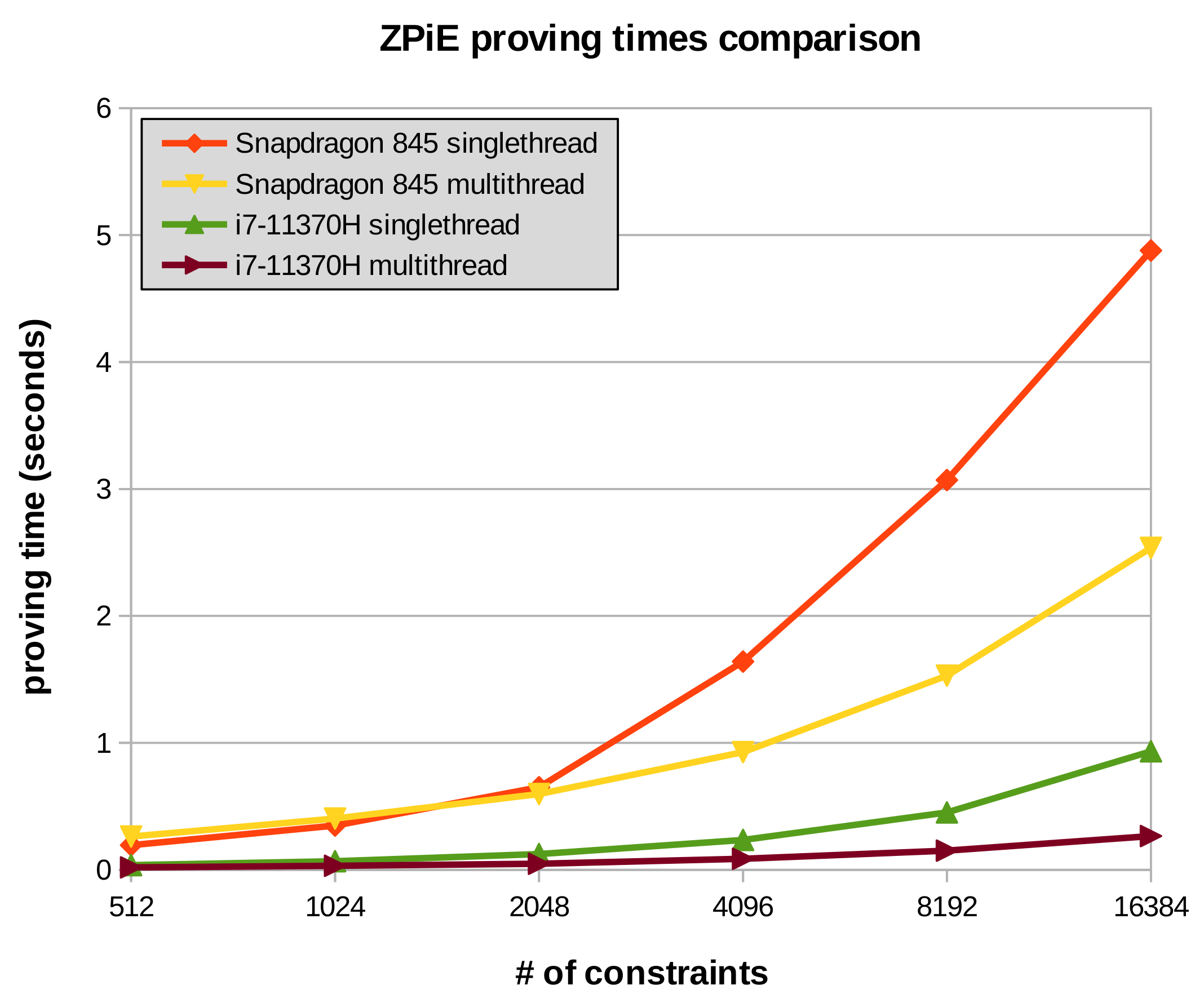
Figure 5. CPUs proving times of ZPiE executed in a Raspberry Pi Zero W. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

Figure 5. CPUs proving times of ZPiE executed in a Raspberry Pi Zero W. The used zk-SNARK is Groth'16, and the elliptic curve BN128.

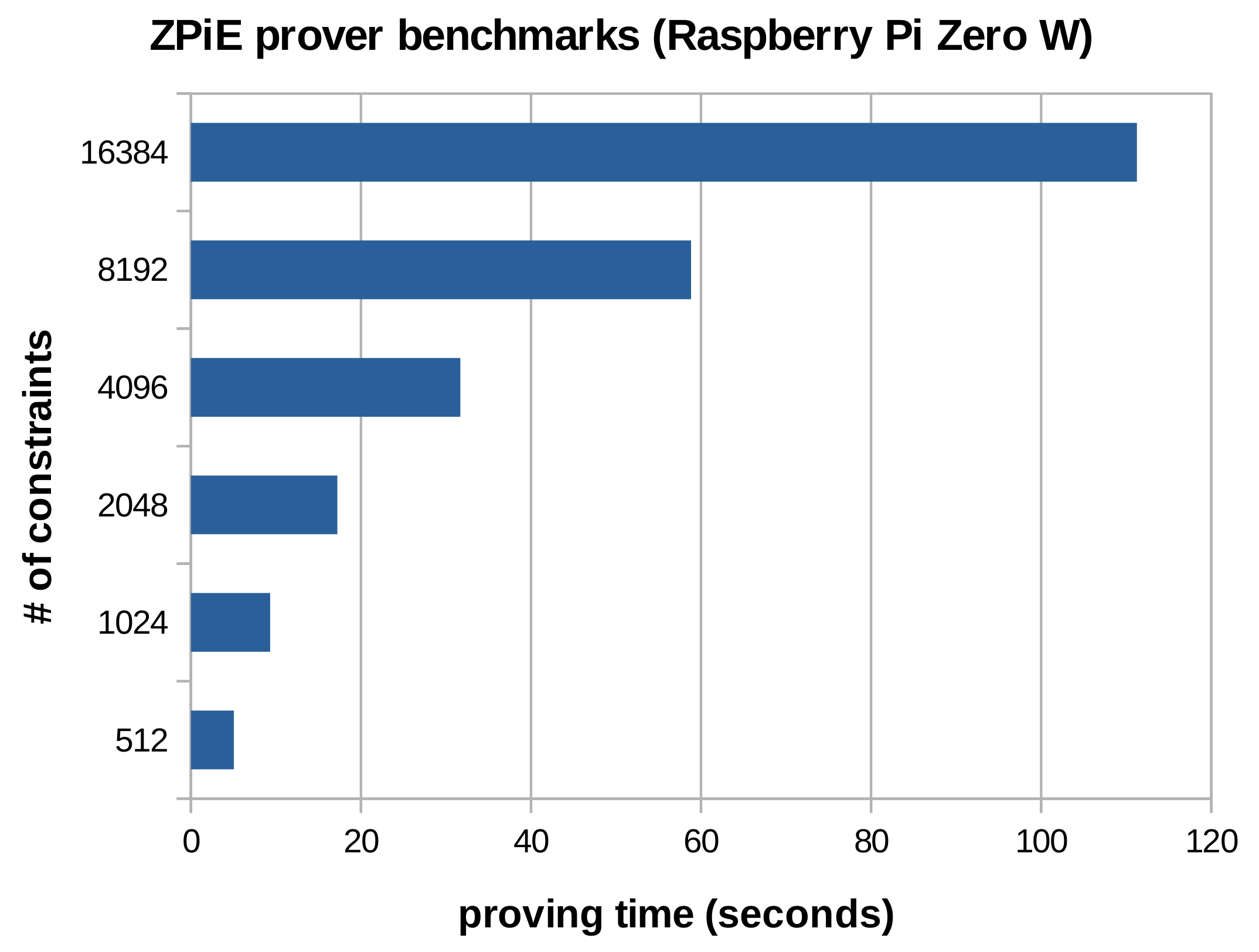
Table 1. Comparison of different ZKP constructions, in regards to their asymptotic efficiency, where n is the number of gates of the circuit and d its depth. (TS = trusted setup, PQS = post-quantum secure,

$\left|\pi \right|=$

proof size,

$\odot =$

per-statement,

$▵=$

updatable).

Table 1. Comparison of different ZKP constructions, in regards to their asymptotic efficiency, where n is the number of gates of the circuit and d its depth. (TS = trusted setup, PQS = post-quantum secure,

$\left|\pi \right|=$

proof size,

$\odot =$

per-statement,

$▵=$

updatable).

Scheme	TS	PQS	Prove	Verify	$\left|\mathit{\pi }\right|$	Security Assumption
BSCTV'13 [17]	⊙	no	$O(nlogn)$	$O\left(1\right)$	$O\left(1\right)$	q-PKE
Groth'16 [18]	⊙	no	$O(nlogn)$	$O\left(1\right)$	$O\left(1\right)$	q-PKE
Sonic [19]	Δ	no	$O(nlogn)$	$O\left(1\right)$	$O\left(1\right)$	AGM
Libra [20]	Δ	no	$O\left(n\right)$	$O(dlogn)$	$O(dlogn)$	q-SBDH, q-PKE
Bulletproofs [23]	no	no	$O\left(n\right)$	$O\left(n\right)$	$O(logn)$	DLP
zk-STARKs [24]	no	yes	$O\left(n{log}^{2}n\right)$	$O\left({log}^{2}n\right)$	$O\left({log}^{2}n\right)$	CRHF

Publisher's Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

We use cookies on our website to ensure you get the best experience.
Read more about our cookies here.

We have just recently launched a new version of our website.
Help us to further improve by taking part in this short 5 minute survey here. here.

Book to Programming With Zero Knowledge

Source: https://www.mdpi.com/2227-7390/9/20/2569/htm

Share :